随机计算(Stochastic Computing)是一种使用随机二进制比特流进行计算的范式,这与 8.1 节中介绍的近似计算的出发点及应用场合比较接近,因为随机本身就是一种近似计算。
随机计算最早是在 20 世纪 60 年代引入的,用于逻辑电路设计,但是其起源可以追溯到冯·诺依曼关于随机逻辑的开创性工作。在随机计算中,实数由通常按时序实现的随机二进制比特流表示,信息承载在二进制比特流的统计信息上。近年来随着量子计算的兴起,人们对于如何采用随机概率来进行计算有了很大的兴趣,因为量子计算就是一种基于概率的计算,它被认为是随机算术处理的一个典型例子。
随机计算有着硬件简单性和容错性之类的优势,这在多种应用的数据处理中得到了证明,如图像处理、频谱变换、可靠性分析等。近年来它也出现在深度学习加速器 AI 芯片的应用中。随机计算的概念已扩展到系统、架构和应用级别的错误恢复设计机制中。
随机计算的电路以比特流的形式串行处理数据。图 8.6 为二进制数转换成随机数的方式,即把给定的二进制数 B 转换为随机比特流形式。由一个随机数生成器生成随机二进制数 R,然后与 B 进行比较后采样,以每个时钟周期 1 比特的速率输出概率为 B/2 k 的随机数。在 N 个时钟周期后,它产生了一个 N 比特长的随机流 X,它的概率 P(X)约等于 B/2 k 。P 值是出现 1 的频率或速率,因此一个 P(X)的估计值可以简单地通过计算 X 中的 1 来估算,估计的准确性取决于 X 的位数的随机性及 N 的长度 [149] 。随机数生成器通常不是真随机源,而是采用逻辑电路,例如线性反馈移位寄存器(Linear Feedback Shift Register,LFSR),其输出是可重复的。
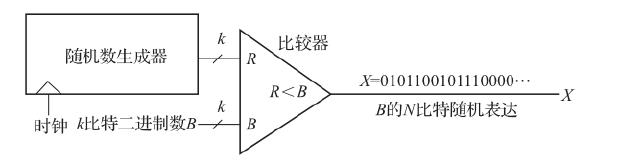 图 8.6 二进制数的随机表达
图 8.6 二进制数的随机表达
在随机计算中,一个随机数是通过对比特流中的 1 进行计数来表示一个实数
(本章节未完结,点击下一页翻页继续阅读)


