最优化问题自然地分成两类:一类是连续变量的问题,另一类是离散变量的问题。在连续变量的问题里,一般是求一组实数,或者一个函数。离散变量的最优化问题被称为组合优化的问题,是从一个无限集或可数无限集里寻找一个对象,典型对象如一个整数、一个集合、一个排列或一个图。
生活中许多问题都是由相互冲突和影响的多个目标组成的。人们会经常遇到使多个目标在给定区域同时尽可能最佳的优化问题。组合优化问题在工程应用等现实生活中非常普遍,并且处于非常重要的地位,这些实际问题通常非常复杂、困难。自 20 世纪 60 年代早期以来,组合优化问题吸引了越来越多不同背景的研究人员的注意力。因此,解决组合优化问题具有非常重要的科研价值和实际意义,尤其是当今 AI 算法和模型的研究中,也有大量优化问题需要解决。
一般情况下,多目标优化问题的各个子目标之间是矛盾的,一个子目标的改善有可能会引起另一个或另几个子目标的性能降低。也就是说,要同时使多个子目标一起达到最优值是不可能的,而只能在它们中间进行协调和折中处理,使各个子目标都尽可能地达到最优化。如果用 f i 代表子目标 i 的成本函数,f=y 代表总成本函数,多目标优化问题的解就是使总成本函数最小。这可以表达为
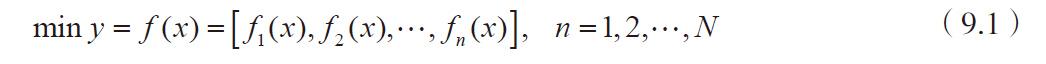
典型的多目标组合优化问题求解思路是对问题进行数学建模,将其抽象为数值函数,选择最佳组合的优化问题。当该函数在连续、可求导、低阶的简单情况下可解析地求出其最优解,但因为各种因素影响复杂,大部分情况下只能进行近似优化计算。尤其当问题规模较大时,优化计算的搜索空间也随之急剧扩大,要求出真正的最优解几乎不可能。使用自然计算算法能够在可接受的时间和精度范围内,求出一种近似最优解。
当人们出行时,可以使用地图搜索连接出发点和目的地的最佳路线。根据不同的目的,可以选择什么是最佳路线,例如可以选择在最短的时间内到达,或交通费用更便宜,以得出最佳组合。
这类问题一个比较著名的例子是旅行商问题(Traveling Salesma
(本章节未完结,点击下一页翻页继续阅读)


