在上一节课中,我们介绍了一种很核心的思维方法论:越变,越不变。你会发现,很多你为了解决问题而付出的努力,恰恰在一个更长期的维度上,构成了维持问题的原因。正如爱因斯坦所说:问题不可能由导致这种问题的思维方式来解决。那么我们要怎么样才能在真正意义上,促成这个问题被解决掉呢?
这节课,我们就来好好讨论一下,第二序的改变是怎么发生的。
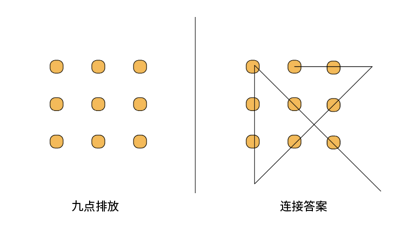
在我为大家介绍的《改变》这本书上,介绍了第二序改变的四个特点。为了说明这些特点,我们先来看一道有趣的数学题,叫做:九点问题。
阐释
可能很多人都看过这道题:一个正方形里,排着9个点。需要你一笔不间断也不重复地,把这9个点都连起来。如果你刚好忘了答案的话,不妨暂停音频,自己试一试。
你可能尝试了很多次,发现每次都差一点,要么就是重复,要么就会差一个点,怎么都不能很顺利地连到一块。但这个问题是有解的,如果你曾经看到过答案,你会觉得很简单:
只要超出这个正方形的范畴,斜着画一把大伞,就刚好把这9个点串起来了。
我们为什么要突然讲一道数学问题呢?
是为了讲这里面的一个思维模式:如果你不知道答案,我相信你刚刚在寻找解决方案的时候,一定是横线竖线斜线,在这个正方形的范围里寻找。而这道题最大的难度,就在于突破这个思维框架,让你发现:哎,没有人说非得在正方形里面啊,我可以把线画到正方形外面去。一旦想到这一点,这道题目就有答案了。这其实是我们第3课讲的「信念」。打破了信念,往往可以带来全新的可能。我们找不到更好的解决方法,往往不是因为我们不够努力,而是解决问题的情境本身受到了限制,我们就要去打破这个情境,跳出这个问题的前提假设。
《改变》这本书,总结了第二序改变的4个特点。这个案例刚好就诠释了这四点。
第一个特点:第二序改变的使用范围,针对的是第一序改变中的问题解决方案。在第一序改变中,我们的解决方案是在正方形当中找思路,而第二序改变
(本章节未完结,点击下一页翻页继续阅读)


