第二节静止的棋盘

「侍立两侧的也为他服务。」

——弥尔顿[1]

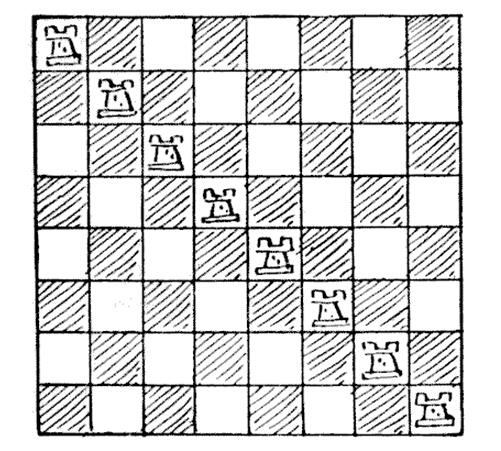
295.八个车

在第一张图中可以看出，棋盘上的每个方格要么被车占领，要么被车攻击，而每个车都被另一个「守卫」（如果它们是黑车和白车相间隔，我们就要称之为「攻击」）。将 8 个车放在任意一行或任意一列显然具有相同的效果。在第二张图中，每个方格也是如此，要么被占领，要么被攻击，但是这里的每个车都没有受到保护。现在将 8 个车放在棋盘上，每个方格要么被占据，要么被攻击，每个车都不会受到另一个的保护，那么一共有多少种放置的方式？我不想让此题卷入反转和映射的问题之中，因此将车放在另一条对角线上可视为一种不同的方式，同样将棋盘调转所得到的重复图形也是不同的方式。

296.四头雄狮

本题是要找出放置 4 头狮子有多少种方式，要求每行或每列都不可多于一头狮子。单靠反转和映射不能视为不同。因此，基于所给出的例子，如果我们将狮子放在另外的对角线上，可以视为相同的排列方式。因为如果你将第二种排列放在镜子前或者旋转 90°，所得到的和第一种排列是一样的。这是一道很简单的小谜题，不过需要非常仔细的思考

297.未受保护的象

将尽可能少的象放在一张普通的棋盘上，以便让棋盘上的每个方格要么被占据，要么被攻击。可以看出，车的势力范围比
（本章节未完结，点击下一页翻页继续阅读）