295.八个车 答案

显然，每一行和每一列上都必须有一个车。从顶行开始，我们可以将第一个车放在 8 个方格中的任意一个里。无论放在哪里，我们在第二行可以有 7 个方格放第二个车。第三行的选择就变成了 6 个方格，第四行的选择是 5 个，以此类推。因此选择的方式为 8×7×6×5×4×3×2×1=40，320（即 8！），也就是正确答案。

如果只是反转和映射的话，不能视为不同的方式，那么一共有多少种方式尚未有定论；这是一道难题。但若是小一号的正方形棋盘，会在下一道题目中进行考量。

296.四头狮子 答案

在这一条件下只存在 7 种不同的方式，分别是：1 2 3 4，1 2 4 3，1 3 2 4，1 3 4 2，1 4 3 2，2 1 4 3，2 4 1 3。以最后一个数列为例，它表示的是我们将一只狮子放在第一行的第 2 个方格，第二行的第 4 个方格，第三行的第 1 个方格，第四行的第 3 个方格。而第一种方式就是我们在题目中所给出的那个。

297.未受保护的象 答案

如果象的数目小于 8 的话，这道题就无解了，最简单的解法是将象沿棋盘第四行或第五行（见图）摆成一条线。但是需要注意，这里的象都不受其它象的保护，因此我们会在下一题中将这一点考虑进去。

298.受保护的象 答案

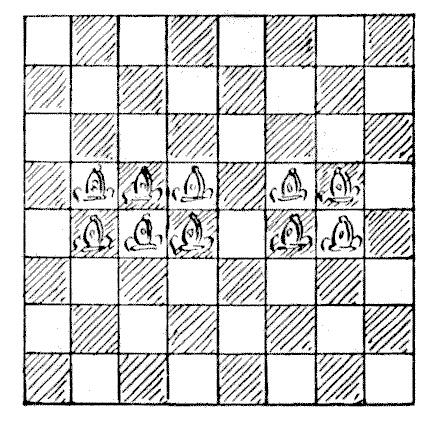
如果你先来思考一下，这道题其实还是很容易的。你只需考虑一种颜色的方格，因为无关白色方格如何处理，总可以用同样的方法处理黑色方格，它们之间是彼此独立的。这种平等正是基于棋盘上的方格数——64——是一个偶数。如果双色棋盘的方格数为奇数，那么一种颜色的方格数总比
（本章节未完结，点击下一页翻页继续阅读）