第十二章 百变的幻方世界

「用神奇的数字吧。」

——康格里夫《悲伤的新娘》[1]

幻方谜题（纵横图谜题）是数学类问题中最历史悠久的一类分支。尽管资料分散，但众多文献中都有记载。幻方谜题的形式非常简单：将连续的整数放置于正方形的各单元格中，使得每行、每列甚至每条主对角线上的数字相加，其和都是同一个数。通过这种简单的形式，可以总结出研究幻方谜题的三条主线：幻方的构造、枚举和分类。

近年来，许多巧妙的方法被运用到幻方谜题的构造上，同时随着人们对幻方谜题的形式理解得越来越透彻，所有古老的谜题已经不再是谜题，而构造各种大小、规格的幻方谜题也不再是难题。于是，人们也鲜少花费精力在幻方的构造上。而「按照某个特定顺序枚举出每一个可行的幻方」却停滞在两百年前。众所周知，三阶幻方有且仅有一种解决方案。1693 年，弗兰尼柯发表著作称四阶乘幻方的所有解决方案一共是 880 种，而他提出的方案也经过了世人的无数次证实。在这里，我所指的是通用的解决方案，它并不要求数字必须是连续的。这个方案由 E.博格特于 1910 年 5 月的《自然》上发表，我认为它对于学习纵横图的读者意义重大。由于更高阶的幻方题解题数目之多，故不可能一一列举。

说到分类，由于这往往涉及规则、数字顺序的美妙性，因此人们对幻方的分类很大程度上取决于个人品味——或者说审美。如同曾几何时，有位绅士将人类分成两大类——吸鼻烟的和不吸鼻烟的。我也无法确定我们对于幻方的分类是否毫无意义，然而，热爱幻方的解题者似乎都在某种程度上同意「纳西克幻方」（由弗罗斯特先生命名，弗罗斯特先生是研究纳西克幻方的学者，他以自己居住过的一个印度小镇名来命名此类幻方，它还被称为「恶魔泛对角幻方」。）以及「联合幻方」的独特趣味性。为了便于初学者理解，我会在这里解释这两种幻方的特点。

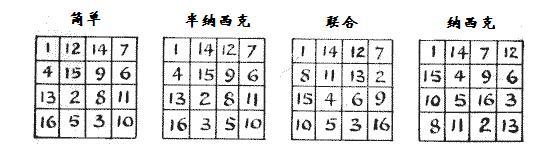
1910 年 1 月 15 日的《女王》杂志刊登了我的一则文章，文章呼吁有意愿的读者将四阶幻方的 880 种
（本章节未完结，点击下一页翻页继续阅读）