第二节质数幻方

关于质数幻方的课题讨论是我本人在 1900 年 7 月 22 日及 8 月 5 日的《每周快讯》中首次提出的。最近这三四年，质数幻方受到了许多美国数学家的重视。起初，他们想要尝试构造出幻和最小的质数幻方。因此，他们采用尽可能小的 9 个质数（包括 1-23 内的质数），使之组成一个幻和为 99（能被 3 整除）的幻方。这个方案在理论上是正确的，然而，有人声称质数幻方最小的幻和应该为 111，而这 9 个质数应该为 1、7、13、31、37、43、61、67、73。同样，在四阶幻方中，「理论上最小幻和」的幻方也被证实是不可行的。可是，在其他阶的幻方（包括 12 阶幻方中），通过理论所得出的最小幻和的幻方却被证实是可行的。而 12 阶幻方则是「所填数字为从 1 开始的连续质数」的最小阶层幻方。换句话说，从 1 开始的前 144 个奇质数可以全部填进 12 格中，构成一个幻方。下面是 1913 年芝加哥的《一元论者》中对质数幻方的总结：

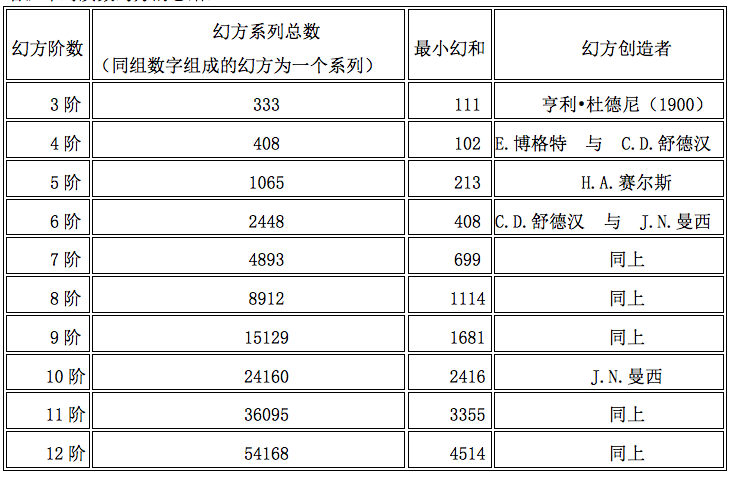
如果读者需要更多详细信息，请参看 W.S.安德鲁与 H.A.曼西的著作。

以上提到的这些研究人员还在构造联合幻方及类似的质数幻方上有显著的成就。舒德汉先生还寄给我一份惊人的研究论文，上面详细地列举了从 4 阶到 10 阶的质数纳西克幻方（除 9 阶以外），之所以没有 3 阶是因为不可能构造出 3 阶的质数纳西克幻方，而没有 9 阶幻方纯粹是因为时间不够充裕的问题。

409.九篮李子

我第一次讨论质数幻方的时，便采用了此题的形式。在这里，我要事先「警告」各位读者，题中有一个小陷阱。

某水果商有 9 个篮子。每个篮
（本章节未完结，点击下一页翻页继续阅读）